Note
Click here to download the full example code
Contributions of up- and downgoing TM- and TE-modes¶
This is an example for the add-on tmtemod. The example is taken from the
CSEM-book by Ziolkowski and Slob, 2019. Have a look at the CSEM-book repository
on empymod/csem-ziolkowski-and-slob for many more examples.
Reference
Ziolkowski, A., and E. Slob, 2019, Introduction to Controlled-Source Electromagnetic Methods: Cambridge University Press; ISBN 9781107058620.
import empymod
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
Model parameters¶
# Offsets
x = np.linspace(10, 1.5e4, 128)
# Resistivity model
rtg = [2e14, 1/3, 1, 70, 1] # With target
rhs = [2e14, 1/3, 1, 1, 1] # Half-space
# Common model parameters (deep sea parameters)
model = {
'src': [0, 0, 975], # Source location
'rec': [x, x*0, 1000], # Receiver location
'depth': [0, 1000, 2000, 2040], # 1 km water, target 40 m thick 1 km below
'freqtime': 0.5, # Frequencies
'verb': 1, # Verbosity
}
Computation¶
target = empymod.dipole(res=rtg, **model)
tgTM, tgTE = empymod.tmtemod.dipole(res=rtg, **model)
# Without reservoir
notarg = empymod.dipole(res=rhs, **model)
ntTM, ntTE = empymod.tmtemod.dipole(res=rhs, **model)
Figure 1¶
Plot all reflected contributions (without direct field), for the models with and without a reservoir.
plt.figure(figsize=(10, 4))
# 1st subplot
ax1 = plt.subplot(121)
plt.semilogy(x/1000, np.abs(tgTE[0]), 'C0-.')
plt.semilogy(x/1000, np.abs(ntTE[0]), 'k-.', label='TE$^{--}$')
plt.semilogy(x/1000, np.abs(tgTE[2]), 'C0-')
plt.semilogy(x/1000, np.abs(ntTE[2]), 'k-', label='TE$^{+-}$')
plt.semilogy(x/1000, np.abs(tgTE[1]), 'C0--')
plt.semilogy(x/1000, np.abs(ntTE[1]), 'k--', label='TE$^{-+}$')
plt.semilogy(x/1000, np.abs(tgTE[3]), 'C0:')
plt.semilogy(x/1000, np.abs(ntTE[3]), 'k:', label='TE$^{++}$')
plt.semilogy(-1, 1, 'k-', label='No target') # Dummy entries for labels
plt.semilogy(-1, 1, 'C0-', label='Target') # "
plt.legend()
plt.xlabel('Offset (km)')
plt.ylabel('Electric field amplitude (V/m)')
plt.xlim([0, 15])
# 2nd subplot
plt.subplot(122, sharey=ax1)
plt.semilogy(x/1000, np.abs(tgTM[0]), 'C0-.')
plt.semilogy(x/1000, np.abs(ntTM[0]), 'k-.', label='TM$^{--}$')
plt.semilogy(x/1000, np.abs(tgTM[2]), 'C0-')
plt.semilogy(x/1000, np.abs(ntTM[2]), 'k-', label='TM$^{+-}$')
plt.semilogy(x/1000, np.abs(tgTM[1]), 'C0--')
plt.semilogy(x/1000, np.abs(ntTM[1]), 'k--', label='TM$^{-+}$')
plt.semilogy(x/1000, np.abs(tgTM[3]), 'C0:')
plt.semilogy(x/1000, np.abs(ntTM[3]), 'k:', label='TM$^{++}$')
plt.semilogy(-1, 1, 'k-', label='No target') # Dummy entries for labels
plt.semilogy(-1, 1, 'C0-', label='Target') # "
plt.legend()
plt.xlabel('Offset (km)')
plt.ylim([1e-17, 1e-9])
plt.xlim([0, 15])
plt.show()
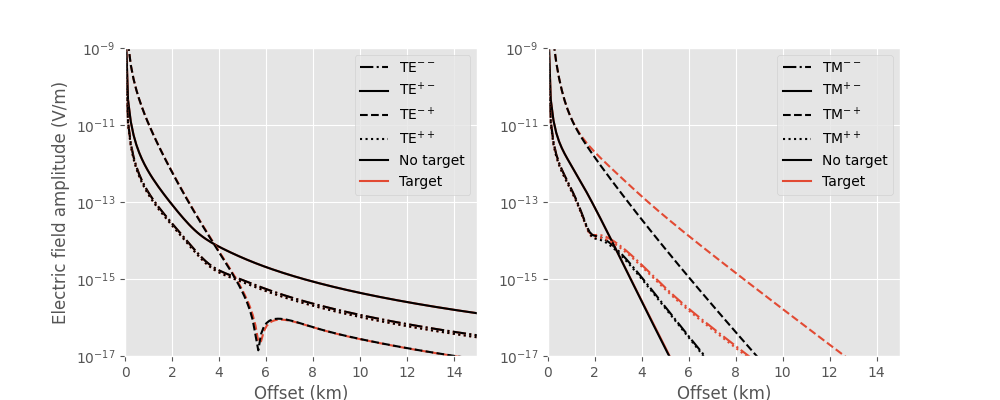
The result shows that mainly the TM-mode contributions are sensitive to the reservoir. For TM, all modes contribute significantly except $T^{+-}$, which is the field that travels upwards from the source and downwards to the receiver.
Figure 2¶
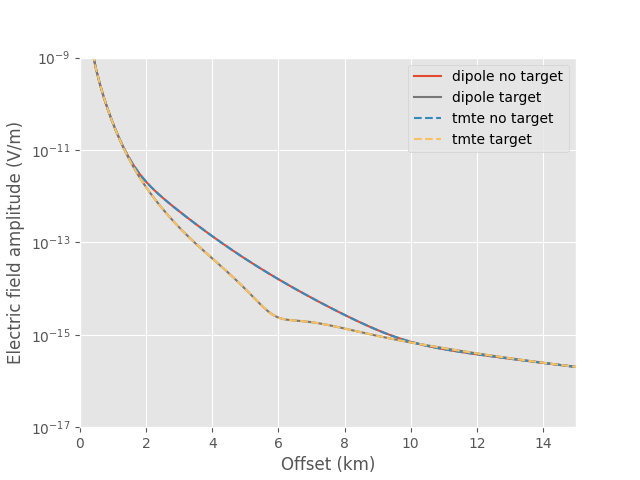
Finally we check if the result from empymod.dipole equals the sum of the
output of empymod.tmtemod.dipole.
plt.figure()
nt = ntTM[0]+ntTM[1]+ntTM[2]+ntTM[3]+ntTM[4]
nt += ntTE[0]+ntTE[1]+ntTE[2]+ntTE[3]+ntTE[4]
tg = tgTM[0]+tgTM[1]+tgTM[2]+tgTM[3]+tgTM[4]
tg += tgTE[0]+tgTE[1]+tgTE[2]+tgTE[3]+tgTE[4]
plt.semilogy(x/1000, np.abs(target), 'C0-', label='dipole no target')
plt.semilogy(x/1000, np.abs(notarg), 'C3-', label='dipole target')
plt.semilogy(x/1000, np.abs(tg), 'C1--', label='tmte no target')
plt.semilogy(x/1000, np.abs(nt), 'C4--', label='tmte target')
plt.legend()
plt.xlabel('Offset (km)')
plt.ylabel('Electric field amplitude (V/m)')
plt.ylim([1e-17, 1e-9])
plt.xlim([0, 15])
plt.show()
empymod.Report()
Total running time of the script: ( 0 minutes 2.084 seconds)
Estimated memory usage: 9 MB