Note
Click here to download the full example code
DC apparent resistivity¶
DC apparent resistivity, dipole-dipole configuration.
There are various DC sounding layouts, the most common ones being Schlumberger, Wenner, pole-pole, pole-dipole, and dipole-dipole, at which we have a look here.
Dipole-dipole layout as shown in figure 8.32 in Kearey et al. (2002):
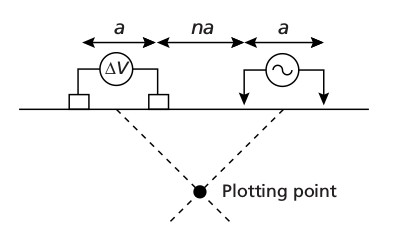
The apparent resistivity \(\rho_a\) of the plotting point is then computed with
where \(V\) is measured Voltage, \(I\) is source strength, \(a\) is dipole length, and \(n\) is the factor of source-receiver separation.
References
Kearey, P., M. Brooks, and I. Hill, 2002, An introduction to geophysical exploration, 3rd ed.: Blackwell Scientific Publications, ISBN: 0 632 04929 4.
import empymod
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
Compute \(\boldsymbol{\rho_a}\)¶
First we define a function to compute apparent resistivity for a given model and given source and receivers.
def comp_appres(depth, res, a, n, srcpts=1, recpts=1, verb=1):
"""Return apparent resistivity for dipole-dipole DC measurement
rho_a = V/I pi a n (n+1) (n+2).
Returns die apparent resistivity due to:
- Electric source, inline (y = 0 m).
- Source of 1 A strength.
- Source and receiver are located at the air-interface.
- Source is centered at x = 0 m.
Note: DC response can be obtained by either t->infinity s or f->0 Hz. f = 0
Hz is much faster, as there is no Fourier transform involved and only
a single frequency has to be computed. By default, the minimum
frequency in empymod is 1e-20 Hz. The difference between the signals
for 1e-20 Hz and 0 Hz is very small.
For more explanation regarding input parameters see `empymod.model`.
Parameters
----------
depth : Absolute depths of layer interfaces, without air-interface.
res : Resistivities of the layers, one more than depths (lower HS).
a : Dipole length.
n : Separation factors.
srcpts, recpts : If < 3, bipoles are approximated as dipoles.
verb : Verbosity.
Returns
-------
rho_a : Apparent resistivity.
AB2 : Src/rec-midpoints
"""
# Get offsets between src-midpoint and rec-midpoint, AB
AB = (n+1)*a
# Collect model, putting source and receiver slightly (1e-3 m) into the
# ground.
model = {
'src': [-a/2, a/2, 0, 0, 1e-3, 1e-3],
'rec': [AB-a/2, AB+a/2, AB*0, AB*0, 1e-3, 1e-3],
'depth': np.r_[0, np.array(depth, ndmin=1)],
'freqtime': 1e-20, # Smaller f would be set to 1e-20 be empymod.
'verb': verb, # Setting it to 1e-20 avoids warning-message.
'res': np.r_[2e14, np.array(res, ndmin=1)],
'strength': 1, # So it is NOT normalized to 1 m src/rec.
'htarg': {'pts_per_dec': -1},
}
return np.real(empymod.bipole(**model))*np.pi*a*n*(n+1)*(n+2), AB/2
Plot-function¶
Second we create a plot-function, which includes the call to comp_appres, to use for a couple of different models.
def plotit(depth, a, n, res1, res2, res3, title):
"""Call `comp_appres` and plot result."""
# Compute the three different models
rho1, AB2 = comp_appres(depth, res1, a, n)
rho2, _ = comp_appres(depth, res2, a, n)
rho3, _ = comp_appres(depth, res3, a, n)
# Create figure
plt.figure()
# Plot curves
plt.loglog(AB2, rho1, label='Case 1')
plt.plot(AB2, rho2, label='Case 2')
plt.plot(AB2, rho3, label='Case 3')
# Legend, labels
plt.legend(loc='best')
plt.title(title)
plt.xlabel('AB/2 (m)')
plt.ylabel(r'Apparent resistivity $\rho_a (\Omega\,$m)')
plt.show()
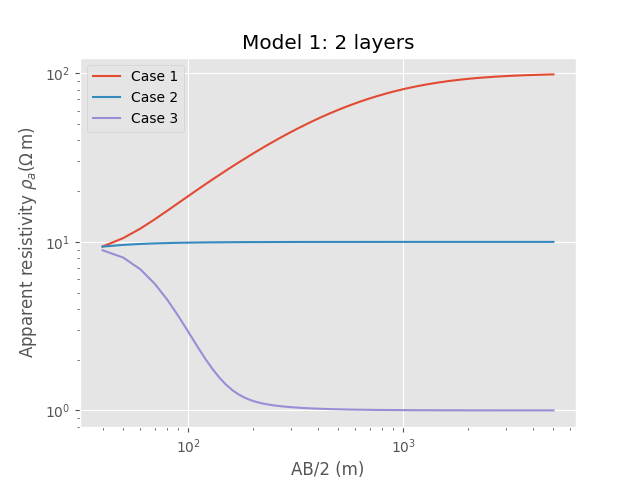
Model 1: 2 layers¶
layer |
depth (m) |
resistivity (Ohm m) |
|---|---|---|
air |
\(-\infty\) - 0 |
2e14 |
layer 1 |
0 - 50 |
10 |
layer 2 |
50 - \(\infty\) |
100 / 10 / 1 |
plotit(
50, # Depth
20, # a (src- and rec-lengths)
np.arange(3, 500), # n
[10, 100], # Case 1
[10, 10], # Case 2
[10, 1], # Case 3
'Model 1: 2 layers')
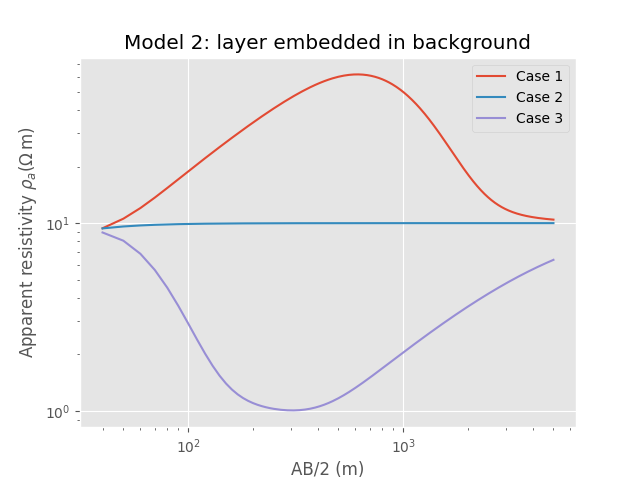
Model 2: layer embedded in background¶
layer |
depth (m) |
resistivity (Ohm m) |
|---|---|---|
air |
\(-\infty\) - 0 |
2e14 |
layer 1 |
0 - 50 |
10 |
layer 2 |
50 - 500 |
100 / 10 / 1 |
layer 3 |
500 - \(\infty\) |
10 |
plotit(
[50, 500], # Depth
20, # a (src- and rec-lengths)
np.arange(3, 500), # n
[10, 100, 10], # Case 1
[10, 10, 10], # Case 2
[10, 1, 10], # Case 3
'Model 2: layer embedded in background')
Model 3: 3 layers¶
layer |
depth (m) |
resistivity (Ohm m) |
|
|---|---|---|---|
air |
\(-\infty\) - 0 |
2e14 |
|
layer 1 |
0 - 50 |
10 |
|
layer 2 |
50 - 500 |
100 / 10 / 1 |
|
layer 3 |
500 - \(\infty\) | 1000 / 10 / 0.1 |
||
plotit(
[50, 500], # Depth
20, # a (src- and rec-lengths)
np.arange(3, 500), # n
[10, 100, 1000], # Case 1
[10, 10, 10], # Case 2
[10, 1, 0.1], # Case 3
'Model 3: 3 layers')

empymod.Report()
Total running time of the script: ( 0 minutes 2.048 seconds)
Estimated memory usage: 11 MB