Note
Go to the end to download the full example code
Comparison of half-space solutions#
Comparing of the functions analytical with dipole for a half-space and
a fullspace-solution, where dipole internally uses kernel.fullspace for
the fullspace solution (xdirect=True), and analytical uses internally
kernel.halfspace. Both in the frequency and in the time domain.
import empymod
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
Time Domain#
Define models#
src = [0, 0, 100]
rec = [2000, 500, 200]
res = [2e14, 2.5]
aniso = [1, 2]
time = np.logspace(-2, 3, 301)
# Collect parameters
inpEM = {'src': src, 'rec': rec, 'freqtime': time, 'verb': 0}
inpEMdip = inpEM.copy()
inpEMdip['htarg'] = {'pts_per_dec': -1}
modHS = {'res': res, 'aniso': aniso}
modFS = {'res': res[1], 'aniso': aniso[1]}
all_abs = [11, 12, 13, 21, 22, 23, 31, 32, 33]
Plot result#
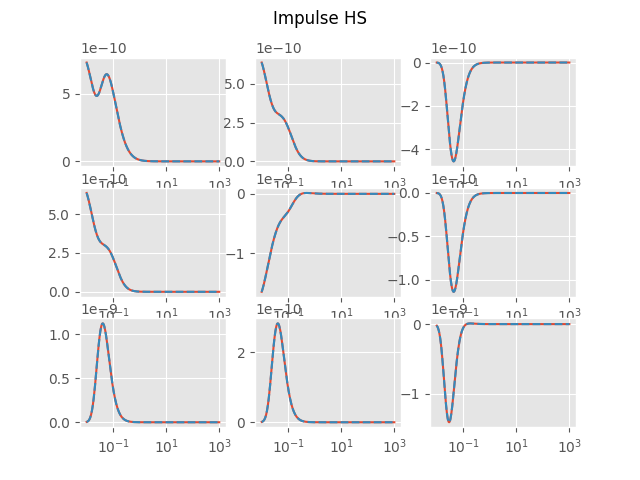
Impulse HS
plt.figure('Impulse HS')
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modHS, ab=ab, signal=0, depth=0)
HS = empymod.analytical(**inpEM, **modFS, solution='dhs', ab=ab, signal=0)
plot_t(EM, HS, 'Impulse HS', i)
plt.suptitle('Impulse HS')
plt.show()
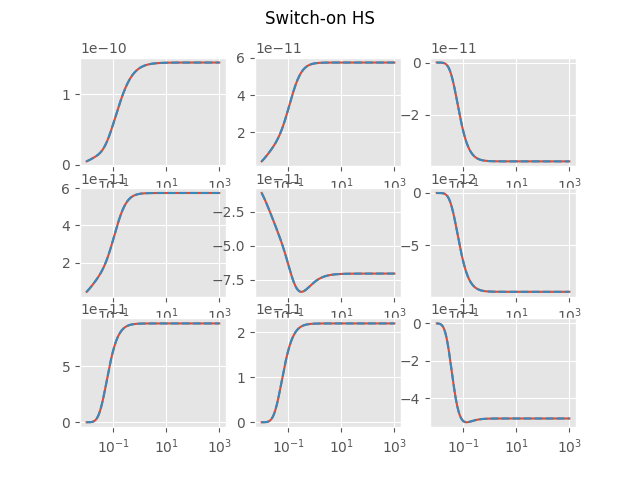
Switch-on HS
plt.figure('Switch-on HS')
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modHS, ab=ab, signal=1, depth=0)
HS = empymod.analytical(**inpEM, **modFS, solution='dhs', ab=ab, signal=1)
plot_t(EM, HS, 'Switch-on HS', i)
plt.suptitle('Switch-on HS')
plt.show()
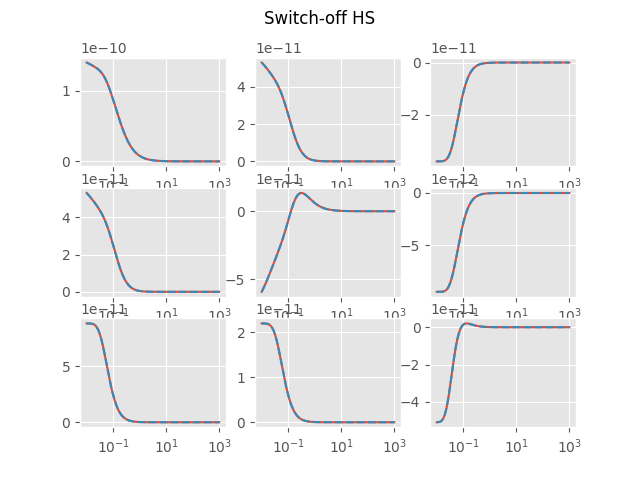
Switch-off HS
plt.figure('Switch-off HS')
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modHS, ab=ab, signal=-1, depth=0)
HS = empymod.analytical(**inpEM, **modFS, solution='dhs', ab=ab, signal=-1)
plot_t(EM, HS, 'Switch-off HS', i)
plt.suptitle('Switch-off HS')
plt.show()
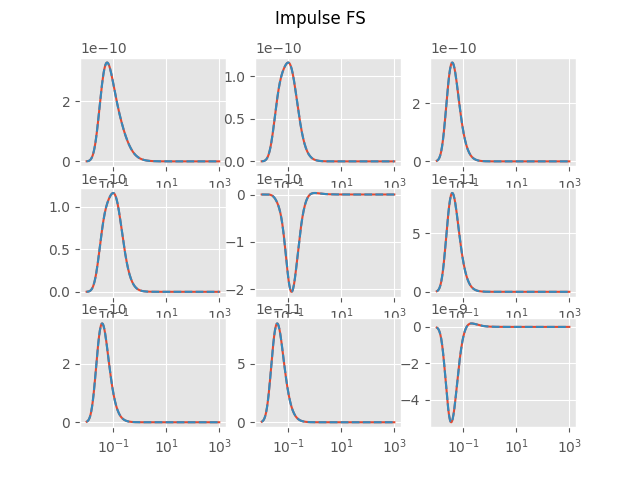
Impulse FS
plt.figure('Impulse FS')
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modFS, ab=ab, signal=0, depth=[])
HS = empymod.analytical(**inpEM, **modFS, solution='dfs', ab=ab, signal=0)
plot_t(EM, HS, 'Impulse FS', i)
plt.suptitle('Impulse FS')
plt.show()
Switch-on FS
plt.figure('Switch-on FS')
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modFS, ab=ab, signal=1, depth=[])
HS = empymod.analytical(**inpEM, **modFS, solution='dfs', ab=ab, signal=1)
plot_t(EM, HS, 'Switch-on FS', i)
plt.suptitle('Switch-on FS')
plt.show()
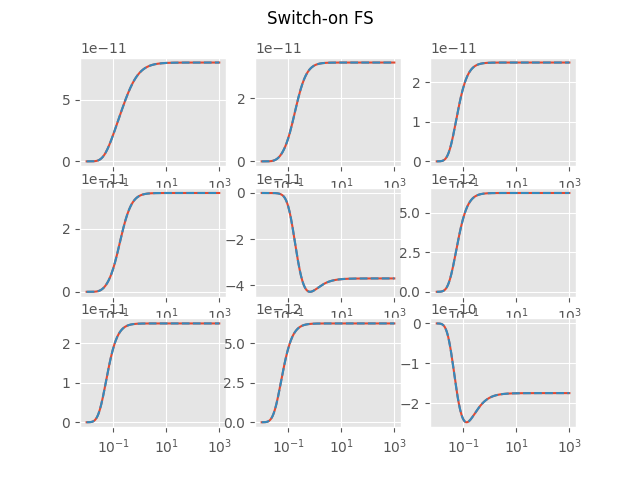
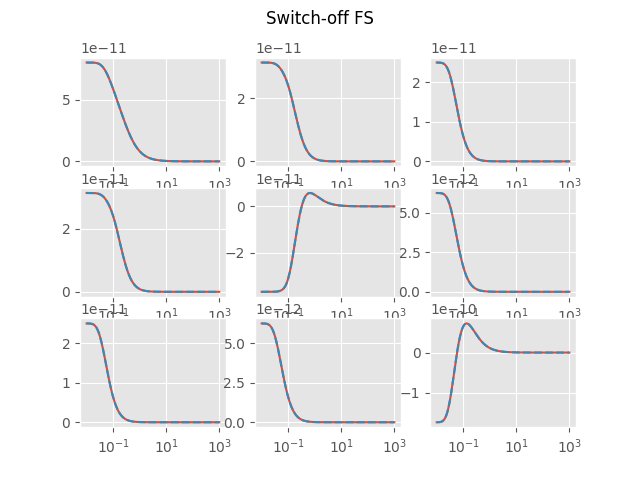
Switch-off FS
plt.figure('Switch-off FS')
i = 330
for ab in all_abs:
i += 1
# Switch-off
EM = empymod.dipole(**inpEMdip, **modFS, ab=ab, signal=-1, depth=[])
HS = empymod.analytical(**inpEM, **modFS, solution='dfs', ab=ab, signal=-1)
plot_t(EM, HS, 'Switch-off FS', i)
plt.suptitle('Switch-off FS')
plt.show()
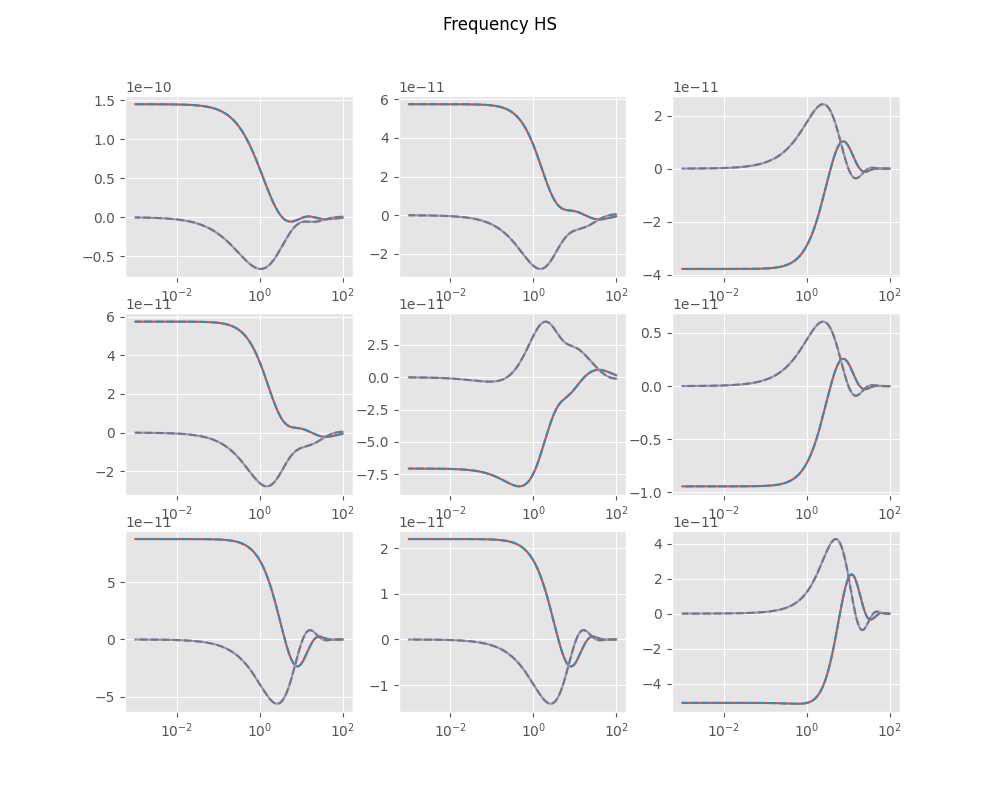
Frequency domain#
Halfspace
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modHS, ab=ab, depth=0)
HS = empymod.analytical(**inpEM, **modFS, solution='dhs', ab=ab)
plot_f(EM, HS, 'Frequency HS', i)
plt.figure('Frequency HS')
plt.suptitle('Frequency HS')
plt.show()
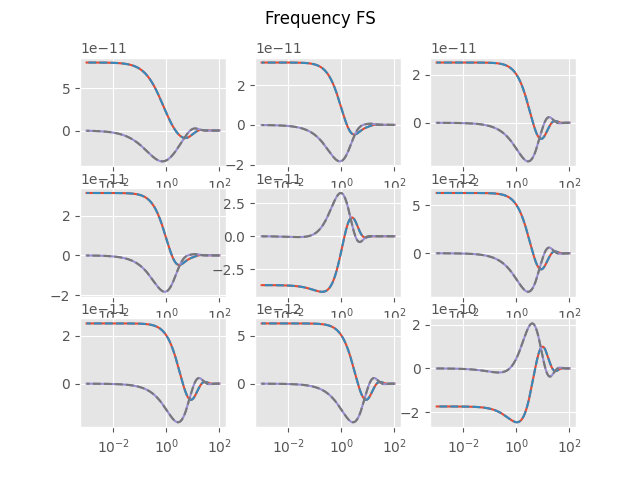
Fullspace
plt.figure('Frequency FS')
i = 330
for ab in all_abs:
i += 1
EM = empymod.dipole(**inpEMdip, **modFS, ab=ab, depth=[])
HS = empymod.analytical(**inpEM, **modFS, solution='dfs', ab=ab)
plot_f(EM, HS, 'Frequency FS', i)
plt.suptitle('Frequency FS')
plt.show()
empymod.Report()
Total running time of the script: (0 minutes 16.498 seconds)
Estimated memory usage: 10 MB