Note
Go to the end to download the full example code
A simple frequency-domain example#
For a single frequency and a crossplot frequency vs offset.
import empymod
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
Define models#
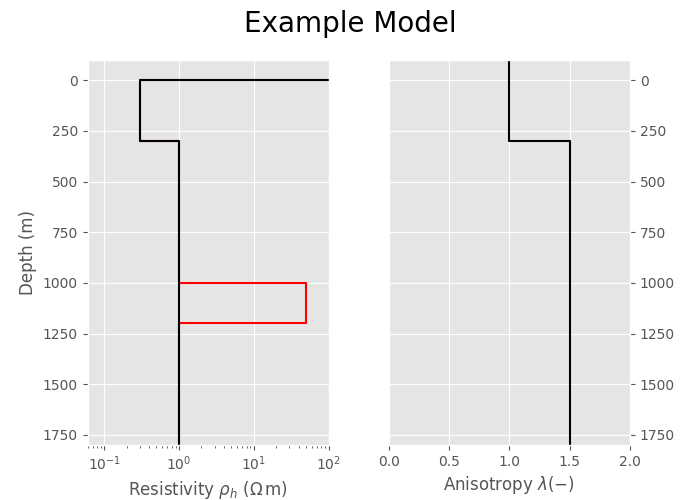
name = 'Example Model' # Model name
depth = [0, 300, 1000, 1200] # Layer boundaries
res = [2e14, 0.3, 1, 50, 1] # Anomaly resistivities
resBG = [2e14, 0.3, 1, 1, 1] # Background resistivities
aniso = [1, 1, 1.5, 1.5, 1.5] # Layer anis. (same for anomaly & backg.)
# Modelling parameters
verb = 0
ab = 11 # source and receiver x-directed
# Spatial parameters
zsrc = 250 # Src-depth
zrec = 300 # Rec-depth
fx = np.arange(20, 101)*100 # Offsets
fy = np.zeros(fx.size) # 0s
Plot models#
pdepth = np.repeat(np.r_[-100, depth], 2)
pdepth[:-1] = pdepth[1:]
pdepth[-1] = 2*depth[-1]
pres = np.repeat(res, 2)
presBG = np.repeat(resBG, 2)
pani = np.repeat(aniso, 2)
# Create figure
fig = plt.figure(figsize=(7, 5), facecolor='w')
fig.subplots_adjust(wspace=.25, hspace=.4)
plt.suptitle(name, fontsize=20)
# Plot Resistivities
ax1 = plt.subplot(1, 2, 1)
plt.plot(pres, pdepth, 'r')
plt.plot(presBG, pdepth, 'k')
plt.xscale('log')
plt.xlim([.2*np.array(res).min(), 2*np.array(res)[1:].max()])
plt.ylim([1.5*depth[-1], -100])
plt.ylabel('Depth (m)')
plt.xlabel(r'Resistivity $\rho_h\ (\Omega\,\rm{m})$')
# Plot anisotropies
ax2 = plt.subplot(1, 2, 2)
plt.plot(pani, pdepth, 'k')
plt.xlim([0, 2])
plt.ylim([1.5*depth[-1], -100])
plt.xlabel(r'Anisotropy $\lambda (-)$')
ax2.yaxis.tick_right()
plt.show()
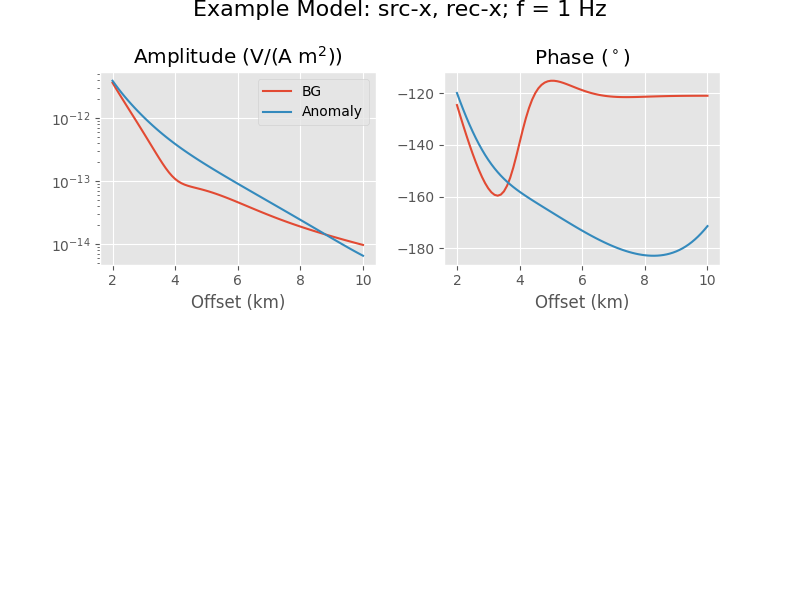
1. Frequency response for f = 1 Hz#
Compute#
Plot#
fig = plt.figure(figsize=(8, 6), facecolor='w')
fig.subplots_adjust(wspace=.25, hspace=.4)
fig.suptitle(name+': src-x, rec-x; f = 1 Hz', fontsize=16, y=1)
# Plot Amplitude
ax1 = plt.subplot(2, 2, 1)
plt.semilogy(fx/1000, fEMBG.amp(), label='BG')
plt.semilogy(fx/1000, fEM.amp(), label='Anomaly')
plt.legend(loc='best')
plt.title(r'Amplitude (V/(A m$^2$))')
plt.xlabel('Offset (km)')
# Plot Phase
ax2 = plt.subplot(2, 2, 2)
plt.title(r'Phase ($^\circ$)')
plt.plot(fx/1000, fEMBG.pha(deg=True), label='BG')
plt.plot(fx/1000, fEM.pha(deg=True), label='Anomaly')
plt.xlabel('Offset (km)')
plt.show()
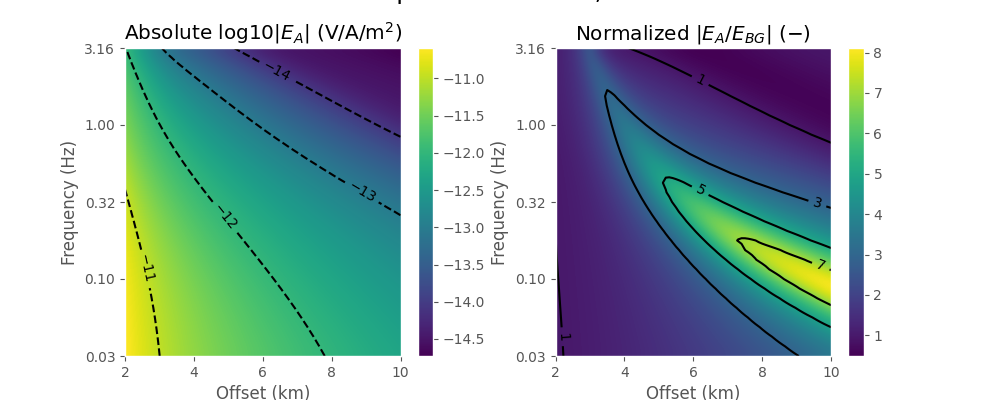
2. Crossplot#
Compute#
# Compute responses
freq = np.logspace(-1.5, .5, 33) # 33 frequencies from -1.5 to 0.5 (logspace)
inpdat = {'src': [0, 0, zsrc], 'rec': [fx, fy, zrec], 'depth': depth,
'freqtime': freq, 'aniso': aniso, 'ab': ab,
'htarg': {'pts_per_dec': -1}, 'verb': verb}
xfEM = empymod.dipole(**inpdat, res=res)
xfEMBG = empymod.dipole(**inpdat, res=resBG)
Plot#
lfreq = np.log10(freq)
# Create figure
fig = plt.figure(figsize=(10, 4), facecolor='w')
fig.subplots_adjust(wspace=.25, hspace=.4)
# Plot absolute (amplitude) in log10
ax1 = plt.subplot(1, 2, 2)
plt.title(r'Normalized $|E_A/E_{BG}|\ (-)$')
plt.imshow(np.abs(xfEM/xfEMBG), interpolation='bicubic',
extent=[fx[0]/1000, fx[-1]/1000, lfreq[0], lfreq[-1]],
origin='lower', aspect='auto')
plt.grid(False)
plt.colorbar()
CS = plt.contour(fx/1000, lfreq, np.abs(xfEM/xfEMBG), [1, 3, 5, 7], colors='k')
plt.clabel(CS, inline=1, fontsize=10)
plt.ylim([lfreq[0], lfreq[-1]])
plt.xlim([fx[0]/1000, fx[-1]/1000])
plt.xlabel('Offset (km)')
plt.ylabel('Frequency (Hz)')
plt.yticks([-1.5, -1, -.5, 0, .5], ('0.03', '0.10', '0.32', '1.00', '3.16'))
# Plot normalized
ax2 = plt.subplot(1, 2, 1)
plt.title(r'Absolute log10$|E_A|$ (V/A/m$^2$)')
plt.imshow(np.log10(np.abs(xfEM)), interpolation='bicubic',
extent=[fx[0]/1000, fx[-1]/1000, lfreq[0], lfreq[-1]],
origin='lower', aspect='auto')
plt.grid(False)
plt.colorbar()
CS = plt.contour(fx/1000, lfreq, np.log10(np.abs(xfEM)),
[-14, -13, -12, -11], colors='k')
plt.clabel(CS, inline=1, fontsize=10)
plt.ylim([lfreq[0], lfreq[-1]])
plt.xlim([fx[0]/1000, fx[-1]/1000])
plt.xlabel('Offset (km)')
plt.ylabel('Frequency (Hz)')
plt.yticks([-1.5, -1, -.5, 0, .5], ('0.03', '0.10', '0.32', '1.00', '3.16'))
fig.suptitle(name+': src-x, rec-x', fontsize=18, y=1.05)
plt.show()
empymod.Report()
Total running time of the script: (0 minutes 1.865 seconds)
Estimated memory usage: 10 MB