Note
Go to the end to download the full example code.
Ward and Hohmann, 1988, SEG#
Frequency and time-domain modelling of magnetic loop sources and magnetic receivers.
Reproducing Figures 2.2-2.5, 4.2-4.5, and 4.7-4.8 of Ward and Hohmann (1988): Frequency- and time-domain isotropic solutions for a full-space (2.2-2.5) and a half-space (4.2-4.5, 4.7-4.8), where source and receiver are at the interface. Source is a loop, receiver is a magnetic dipole.
Reference
Ward, S. H., and G. W. Hohmann, 1988, Electromagnetic theory for geophysical applications, Chapter 4 of Electromagnetic Methods in Applied Geophysics: SEG, Investigations in Geophysics No. 3, 130–311; DOI: 10.1190/1.9781560802631.ch4.
import empymod
import numpy as np
from scipy.special import erf
import matplotlib.pyplot as plt
from scipy.constants import mu_0
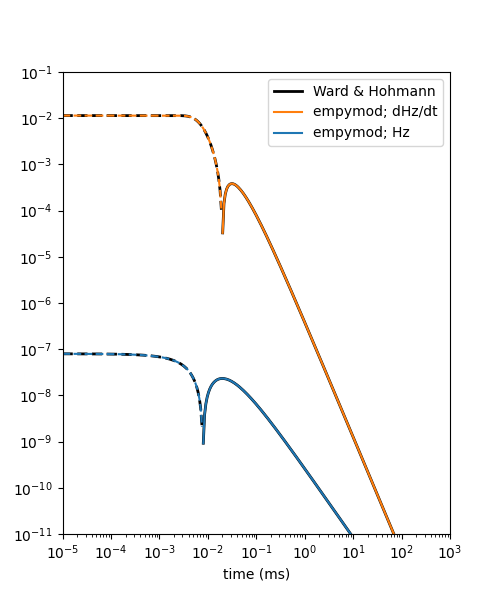
Ward and Hohmann, 1988, Fig 4.4#
Ward and Hohmann (1988), Equations 4.69a and 4.70:
\[h_z = \frac{m}{4\pi r^3} \left[
\frac{9}{2\theta^2 r^2} \rm{erf}(\theta r) - \rm{erf}(\theta r) -
\frac{1}{\pi^{1/2}} \left(\frac{9}{\theta r} + 4\theta r\right)
\exp(-\theta^2 r^2) \right] \, , \qquad (4.69\rm{a})\]
and
\[\frac{\partial h_z}{\partial t} = -\frac{m\rho}{2\pi\mu_0 r^5} \left[
9\rm{erf}(\theta r) -
\frac{2\theta r}{\pi^{1/2}} \left(9 + 6\theta^2 r^2 +
4\theta^4 r^4\right) \exp(-\theta^2 r^2) \right] \, , \qquad (4.70)\]
where
\[\theta = \sqrt{\frac{\mu_0}{4t\rho}} \, ,\]
\(t\) is time in s, \(\rho\) is resistivity in \(\Omega\,\text{m}\), \(r\) is offset in m, and \(m\) the magnetic moment in \(\text{A}\,\text{m}^2\) .
Analytical solutions#
def hz(t, res, r, m=1.):
r"""Return equation 4.69a, Ward and Hohmann, 1988.
Switch-off response (i.e., Hz(t)) of a homogeneous isotropic half-space,
where the vertical magnetic source and receiver are at the interface.
Parameters
----------
t : array
Times (t)
res : float
Halfspace resistivity (Ωm)
r : float
Offset (m)
m : float, optional
Magnetic moment, default is 1.
Returns
-------
hz : array
Vertical magnetic field (A/m)
"""
theta = np.sqrt(mu_0/(4*res*t))
theta_r = theta*r
s = 9/(2*theta_r**2)*erf(theta_r) - erf(theta_r)
s -= (9/theta_r+4*theta_r)*np.exp(-theta_r**2)/np.sqrt(np.pi)
s *= m/(4*np.pi*r**3)
return s
def dhzdt(t, res, r, m=1.):
r"""Return equation 4.70, Ward and Hohmann, 1988.
Impulse response (i.e., dHz(t)/dt) of a homogeneous isotropic half-space,
where the vertical magnetic source and receiver are at the interface.
Parameters
----------
t : array
Times (t)
res : float
Halfspace resistivity (Ωm)
r : float
Offset (m)
m : float, optional
Magnetic moment, default is 1.
Returns
-------
dhz : array
Time-derivative of the vertical magnetic field (A/m/s)
"""
theta = np.sqrt(mu_0/(4*res*t))
theta_r = theta*r
s = (9 + 6 * theta_r**2 + 4 * theta_r**4) * np.exp(-theta_r**2)
s *= -2 * theta_r / np.sqrt(np.pi)
s += 9 * erf(theta_r)
s *= -(m*res)/(2*np.pi*mu_0*r**5)
return s
Analytical result#
Numerical result#
inp1 = {
'src': [0, 0, 0, 0, 90],
'rec': [offset, 0, 0, 0, 90],
'depth': 0,
'res': [2e24, resistivity],
'freqtime': time,
'verb': 1,
'xdirect': True,
'epermH': [0, 0], # Reduce early time numerical noise (diff. approx.)
}
hz_num = empymod.loop(signal=-1, **inp1)
dhz_num = empymod.loop(signal=0, **inp1)
Plot the result#
fig1, ax1 = plt.subplots(1, 1, figsize=(5, 6))
ax1.loglog(time*1e3, pos(dhz_ana), 'k-', lw=2, label='Ward & Hohmann')
ax1.loglog(time*1e3, pos(-dhz_ana), 'k--', lw=2)
ax1.loglog(time*1e3, pos(dhz_num), 'C1-', label='empymod; dHz/dt')
ax1.loglog(time*1e3, pos(-dhz_num), 'C1--')
ax1.loglog(time*1e3, pos(hz_ana), 'k-', lw=2)
ax1.loglog(time*1e3, pos(-hz_ana), 'k--', lw=2)
ax1.loglog(time*1e3, pos(hz_num), 'C0-', label='empymod; Hz')
ax1.loglog(time*1e3, pos(-hz_num), 'C0--')
ax1.set_xlim([1e-5, 1e3])
ax1.set_yticks(10**np.arange(-11., 0))
ax1.set_ylim([1e-11, 1e-1])
ax1.set_xlabel('time (ms)')
ax1.legend()
Original Figure#
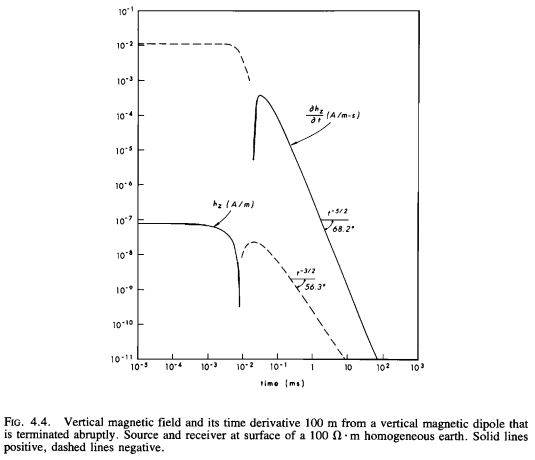
Note that \(h_z\) has the opposite sign in the original figure, which is probably a typo (it is not what their equation yields).
The following examples are just compared to the figures, without the provided analytical solutions.
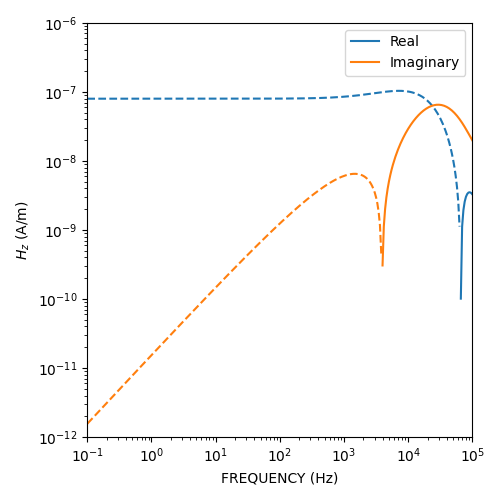
Ward and Hohmann, 1988, Fig 4.2#
# Frequencies
freq = np.logspace(-1, 5, 301)
# Computation
fhz_num = empymod.loop(
src=[0, 0, 0, 0, 90],
rec=[100, 0, 0, 0, 90],
depth=0,
res=[2e14, 100],
freqtime=freq,
verb=1,
)
# Figure
fig2, ax2 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax2.loglog(freq, pos(fhz_num.real), 'C0-', label='Real')
ax2.loglog(freq, pos(-fhz_num.real), 'C0--')
ax2.loglog(freq, pos(fhz_num.imag), 'C1-', label='Imaginary')
ax2.loglog(freq, pos(-fhz_num.imag), 'C1--')
ax2.axis([1e-1, 1e5, 1e-12, 1e-6])
ax2.set_xlabel('FREQUENCY (Hz)')
ax2.set_ylabel('Hz (A/m)')
ax2.legend()
Original Figure#
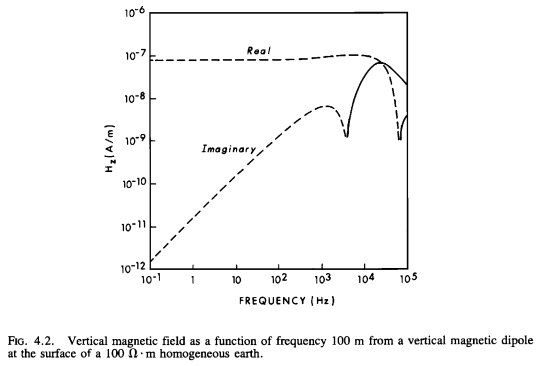
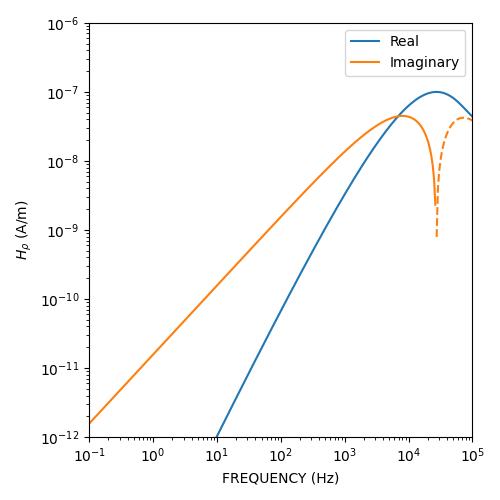
Ward and Hohmann, 1988, Fig 4.3#
# Frequencies
freq = np.logspace(-1, 5, 301)
# Computation
fhz_num = empymod.loop(
src=[0, 0, 0, 0, 90],
rec=[100, 0, 0, 0, 0],
depth=0,
res=[2e14, 100],
freqtime=freq,
verb=1,
)
# Figure
fig3, ax3 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax3.loglog(freq, pos(fhz_num.real), 'C0-', label='Real')
ax3.loglog(freq, pos(-fhz_num.real), 'C0--')
ax3.loglog(freq, pos(fhz_num.imag), 'C1-', label='Imaginary')
ax3.loglog(freq, pos(-fhz_num.imag), 'C1--')
ax3.axis([1e-1, 1e5, 1e-12, 1e-6])
ax3.set_xlabel('FREQUENCY (Hz)')
ax3.set_ylabel('Hρ (A/m)')
ax3.legend()
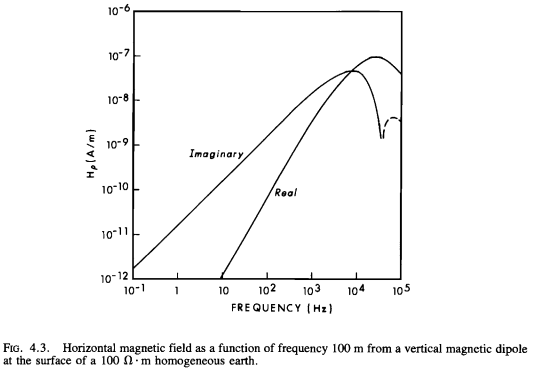
Original Figure#
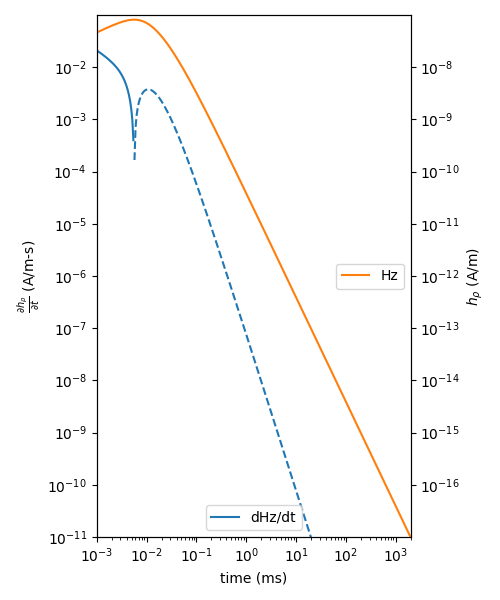
Ward and Hohmann, 1988, Fig 4.5#
# Times
time = np.logspace(-6, 0.5, 301)
# Computation
inp4 = {
'src': [0, 0, 0, 0, 90],
'rec': [100, 0, 0, 0, 0],
'depth': 0,
'res': [2e14, 100],
'epermH': [0, 0],
'freqtime': time,
'verb': 1,
}
fhz_num = empymod.loop(signal=1, **inp4)
fdhz_num = empymod.loop(signal=0, **inp4)
# Figure
fig4, ax4 = plt.subplots(1, 1, figsize=(5, 6), constrained_layout=True)
ax4.loglog(time*1e3, pos(fdhz_num), 'C0-', label='dHz/dt')
ax4.loglog(time*1e3, pos(-fdhz_num), 'C0--')
ax4.axis([1e-3, 2e3, 1e-11, 1e-1])
ax4.set_yticks(10**np.arange(-11., -1))
ax4.set_xlabel('time (ms)')
ax4.set_ylabel('∂hρ/∂t (A/m-s)')
ax4.legend(loc=8)
ax4b = ax4.twinx()
ax4b.loglog(time*1e3, pos(fhz_num), 'C1-', label='Hz')
ax4b.loglog(time*1e3, pos(-fhz_num), 'C1--')
ax4b.axis([1e-3, 2e3, 1e-17, 1e-7])
ax4b.set_yticks(10**np.arange(-16., -7))
ax4b.set_ylabel('hρ (A/m)')
ax4b.legend(loc=5)
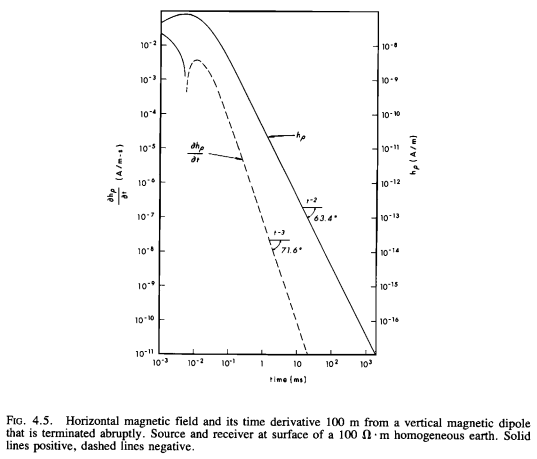
Original Figure#
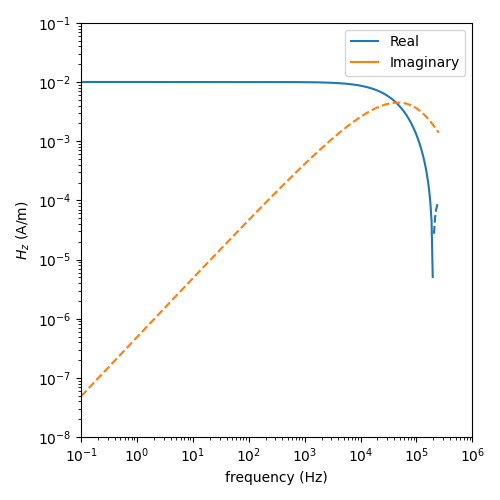
Ward and Hohmann, 1988, Fig 4.7#
# Frequencies and loop characteristics
freq = np.logspace(-1, np.log10(250000), 301)
radius = 50
area = radius**2*np.pi
# Computation
fhz_num = empymod.bipole(
src=[radius, 0, 0, 90, 0],
rec=[0, 0, 0, 0, 90],
depth=0,
res=[2e14, 100],
freqtime=freq,
strength=area/(radius/2),
mrec=True,
verb=1,
)
# Figure
fig5, ax5 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax5.loglog(freq, pos(fhz_num.real), 'C0-', label='Real')
ax5.loglog(freq, pos(-fhz_num.real), 'C0--')
ax5.loglog(freq, pos(fhz_num.imag), 'C1-', label='Imaginary')
ax5.loglog(freq, pos(-fhz_num.imag), 'C1--')
ax5.axis([1e-1, 1e6, 1e-8, 1e-1])
ax5.set_xlabel('frequency (Hz)')
ax5.set_ylabel('Hz (A/m)')
ax5.legend()
Original Figure#
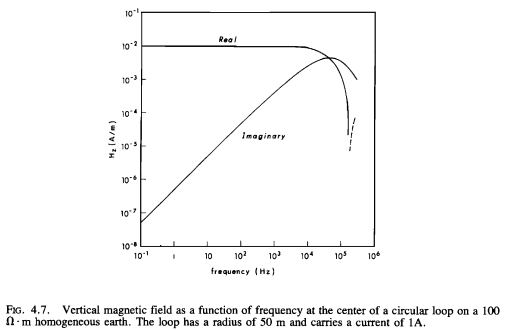
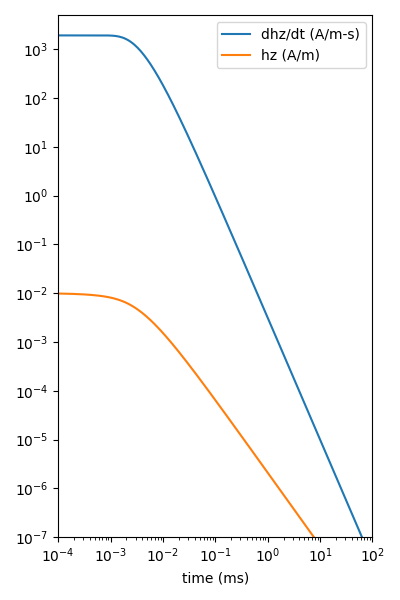
Ward and Hohmann, 1988, Fig 4.8#
# Times and loop characteristics
time = np.logspace(-7, -1, 301)
radius = 50
area = radius**2*np.pi
# Computation
inp6 = {
'src': [radius, 0, 0, 90, 0],
'rec': [0, 0, 0, 0, 90],
'depth': 0,
'res': [2e14, 100],
'freqtime': time,
'strength': area/(radius/2),
'mrec': True,
'epermH': [0, 0],
'verb': 1,
}
fhz_num = empymod.bipole(signal=-1, **inp6)
fdhz_num = empymod.bipole(signal=0, **inp6)
# Figure
fig6, ax6 = plt.subplots(1, 1, figsize=(4, 6), constrained_layout=True)
ax6.loglog(time*1e3, pos(fdhz_num), 'C0-', label='dhz/dt (A/m-s)')
ax6.loglog(time*1e3, pos(-fdhz_num), 'C0--')
ax6.plot(time*1e3, pos(fhz_num), 'C1-', label='hz (A/m)')
ax6.plot(time*1e3, pos(-fhz_num), 'C1--')
ax6.axis([1e-4, 1e2, 1e-7, 5e3])
ax6.set_yticks(10**np.arange(-7., 4))
ax6.set_xlabel('time (ms)')
ax6.legend()
Original Figure#
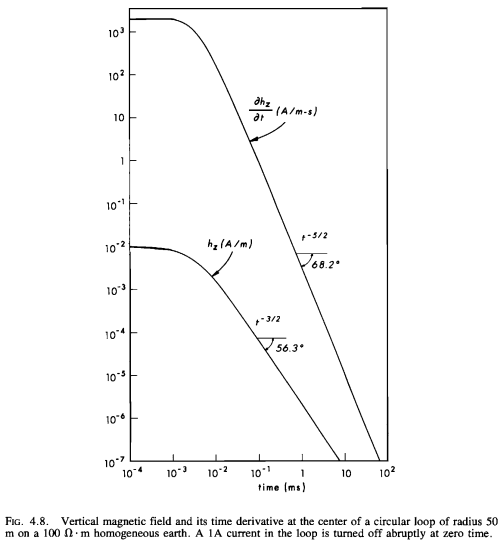
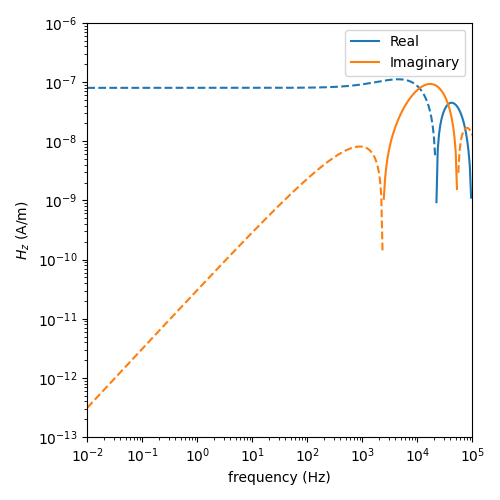
Ward and Hohmann, 1988, Fig 2.2#
# Frequencies
freq = np.logspace(-2, 5, 301)
# Computation
fhz_num = empymod.loop(
src=[0, 0, 0, 0, 0],
rec=[0, 100, 0, 0, 0],
depth=[],
res=100,
freqtime=freq,
verb=1,
)
# Figure
fig7, ax7 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax7.loglog(freq, pos(fhz_num.real), 'C0-', label='Real')
ax7.loglog(freq, pos(-fhz_num.real), 'C0--')
ax7.loglog(freq, pos(fhz_num.imag), 'C1-', label='Imaginary')
ax7.loglog(freq, pos(-fhz_num.imag), 'C1--')
ax7.axis([1e-2, 1e5, 1e-13, 1e-6])
ax7.set_xlabel('frequency (Hz)')
ax7.set_ylabel('Hz (A/m)')
ax7.legend()
Original Figure#
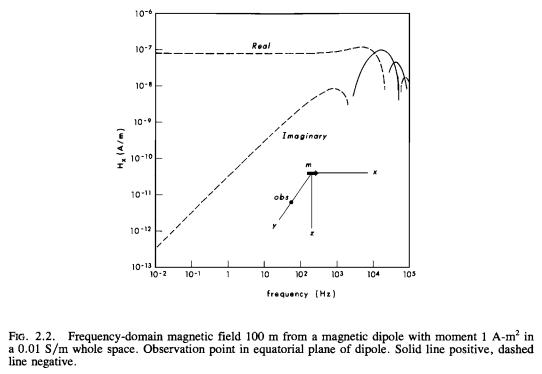
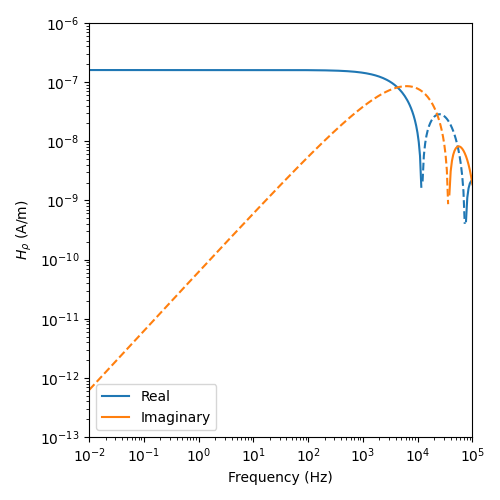
Ward and Hohmann, 1988, Fig 2.3#
# Frequencies
freq = np.logspace(-2, 5, 301)
# Computation
fhz_num = empymod.loop(
src=[0, 0, 0, 0, 0],
rec=[100, 0, 0, 0, 0],
depth=[],
res=100,
freqtime=freq,
verb=1,
)
# Figure
fig8, ax8 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax8.loglog(freq, pos(fhz_num.real), 'C0-', label='Real')
ax8.loglog(freq, pos(-fhz_num.real), 'C0--')
ax8.loglog(freq, pos(fhz_num.imag), 'C1-', label='Imaginary')
ax8.loglog(freq, pos(-fhz_num.imag), 'C1--')
ax8.axis([1e-2, 1e5, 1e-13, 1e-6])
ax8.set_xlabel('Frequency (Hz)')
ax8.set_ylabel('Hρ (A/m)')
ax8.legend()
Original Figure#
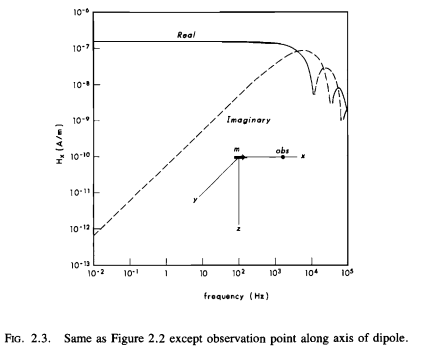
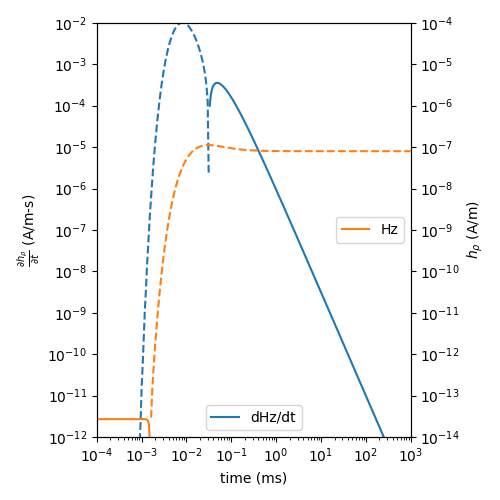
Ward and Hohmann, 1988, Fig 2.4#
# Times
time = np.logspace(-7, 0, 301)
# Computation
inp9 = {
'src': [0, 0, 0, 0, 0],
'rec': [0, 100, 0, 0, 0],
'depth': [],
'res': 100,
'xdirect': True,
'freqtime': time,
'verb': 1,
}
fhz_num = empymod.loop(signal=1, **inp9)
fdhz_num = empymod.loop(signal=0, **inp9)
# Figure
fig9, ax9 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax9.loglog(time*1e3, pos(fdhz_num), 'C0-', label='dHz/dt')
ax9.loglog(time*1e3, pos(-fdhz_num), 'C0--')
ax9.axis([1e-4, 1e3, 1e-12, 1e-2])
ax9.set_yticks(10**np.arange(-12., -1))
ax9.set_xlabel('time (ms)')
ax9.set_ylabel('∂hρ/∂t (A/m-s)')
ax9.legend(loc=8)
ax9b = ax9.twinx()
ax9b.loglog(time*1e3, pos(fhz_num), 'C1-', label='Hz')
ax9b.loglog(time*1e3, pos(-fhz_num), 'C1--')
ax9b.axis([1e-4, 1e3, 1e-14, 1e-4])
ax9b.set_yticks(10**np.arange(-14., -3))
ax9b.set_ylabel('hρ (A/m)')
ax9b.legend(loc=5)
Original Figure#
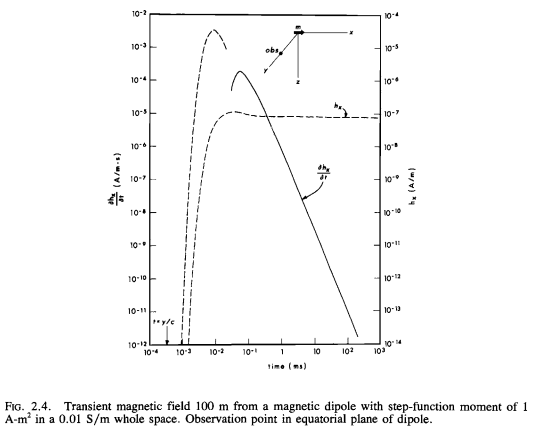
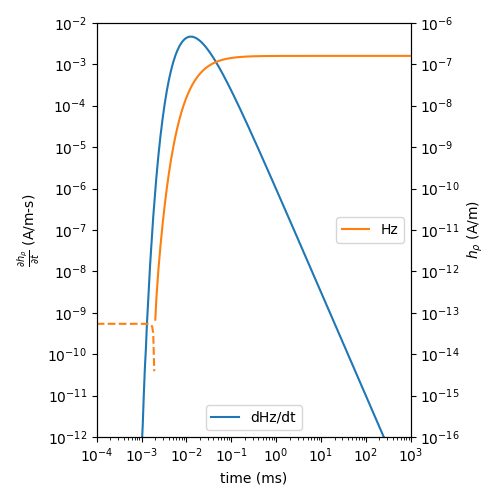
Ward and Hohmann, 1988, Fig 2.5#
# Times
time = np.logspace(-7, 0, 301)
# Computation
inp10 = {
'src': [0, 0, 0, 0, 0],
'rec': [100, 0, 0, 0, 0],
'depth': [],
'res': 100,
'xdirect': True,
'freqtime': time,
'verb': 1,
}
fhz_num = empymod.loop(signal=1, **inp10)
fdhz_num = empymod.loop(signal=0, **inp10)
# Figure
fig10, ax10 = plt.subplots(1, 1, figsize=(5, 5), constrained_layout=True)
ax10.loglog(time*1e3, pos(fdhz_num), 'C0-', label='dHz/dt')
ax10.loglog(time*1e3, pos(-fdhz_num), 'C0--')
ax10.axis([1e-4, 1e3, 1e-12, 1e-2])
ax10.set_yticks(10**np.arange(-12., -1))
ax10.set_xlabel('time (ms)')
ax10.set_ylabel('∂hρ/∂t (A/m-s)')
ax10.legend(loc=8)
ax10b = ax10.twinx()
ax10b.loglog(time*1e3, pos(fhz_num), 'C1-', label='Hz')
ax10b.loglog(time*1e3, pos(-fhz_num), 'C1--')
ax10b.axis([1e-4, 1e3, 1e-16, 1e-6])
ax10b.set_yticks(10**np.arange(-16., -5))
ax10b.set_ylabel('hρ (A/m)')
ax10b.legend(loc=5)
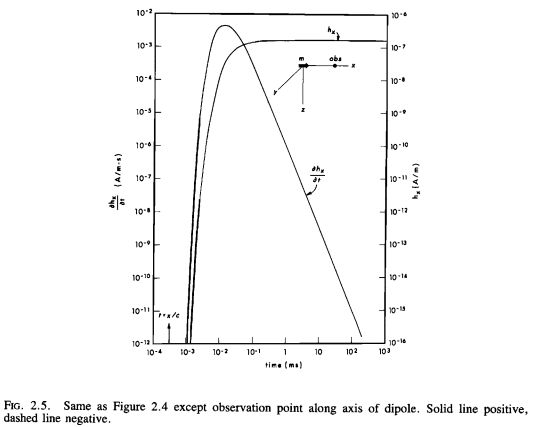
Original Figure#
empymod.Report()
Total running time of the script: (0 minutes 8.442 seconds)
Estimated memory usage: 188 MB