Cole-Cole#

There are various different definitions of a Cole-Cole model, see for instance Tarasov and Titov (2013). We try a few different ones here, but you can supply your preferred version.

The original Cole-Cole (1941) model was formulated for the complex dielectric permittivity. It is reformulated to conductivity to use it for IP,

\[\sigma(\omega) = \sigma_\infty + \frac{\sigma_0 - \sigma_\infty}{1 + (i\omega\tau)^C}\ . \qquad\qquad\qquad (1)\]

Another, similar model is given by Pelton et al. (1978),

\[\rho(\omega) = \rho_\infty + \frac{\rho_0 - \rho_\infty}{1 + (i\omega\tau)^C}\ . \qquad\qquad\qquad (2)\]

Equation (2) is just like equation (1), but replaces \(\sigma\) by \(\rho\). However, mathematically they are not the same. Substituting \(\rho = 1/\sigma\) in the latter and resolving it for \(\sigma\) will not yield the former. Equation (2) is usually written in the following form, using the chargeability \(m = (\rho_0-\rho_\infty)/\rho_0\),

\[\rho(\omega) = \rho_0 \left[1 - m \left(1- \frac{1}{1 + (i\omega\tau)^C} \right)\right]\ . \quad (3)\]

In all cases we add the part coming from the dielectric permittivity (displacement currents), even tough it usually doesn’t matter in the frequency range of IP.

References

Cole, K.S., and R.H. Cole, 1941, Dispersion and adsorption in dielectrics. I. Alternating current characteristics; Journal of Chemical Physics, Volume 9, Pages 341-351, doi: 10.1063/1.1750906.
Pelton, W.H., S.H. Ward, P.G. Hallof, W.R. Sill, and P.H. Nelson, 1978, Mineral discrimination and removal of inductive coupling with multifrequency IP, Geophysics, Volume 43, Pages 588-609, doi: 10.1190/1.1440839.
Tarasov, A., and K. Titov, 2013, On the use of the Cole–Cole equations in spectral induced polarization; Geophysical Journal International, Volume 195, Issue 1, Pages 352-356, doi: 10.1093/gji/ggt251.

import empymod
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')

Use empymod with user-def. func. to adjust \(\eta\) and \(\zeta\)#

In principal it is always best to write your own modelling routine if you want to adjust something. Just copy empymod.dipole or empymod.bipole as a template, and modify it to your needs. Since empymod v1.7.4, however, there is a hook which allows you to modify \(\eta_h, \eta_v, \zeta_h\), and \(\zeta_v\) quite easily.

The trick is to provide a dictionary (we name it inp here) instead of the resistivity vector in res. This dictionary, inp, has two mandatory plus optional entries: - res: the resistivity vector you would have provided normally (mandatory).

A function name, which has to be either or both of (mandatory):
- func_eta: To adjust etaH and etaV, or
- func_zeta: to adjust zetaH and zetaV.
In addition, you have to provide all parameters you use in func_eta/func_zeta and are not already provided to empymod. All additional parameters must have #layers elements.

The functions func_eta and func_zeta must have the following characteristics:

The signature is func(inp, p_dict), where
- inp is the dictionary you provide, and
- p_dict is a dictionary that contains all parameters so far computed in empymod [locals()].
It must return etaH, etaV if func_eta, or zetaH, zetaV if func_zeta.

Dummy example#

def my_new_eta(inp, p_dict):
    # Your computations, using the parameters you provided
    # in ``inp`` and the parameters from empymod in ``p_dict``.
    # In the example below, we provide, e.g., inp['tau']
    return etaH, etaV

And then you call empymod with res = {'res': res-array, 'tau': tau, 'func_eta': my_new_eta}.

Define the Cole-Cole model#

In this notebook we exploit this hook in empymod to compute \(\eta_h\) and \(\eta_v\) with the Cole-Cole model. By default, \(\eta_h\) and \(\eta_v\) are computed like this:

\[\begin{split}\eta_h = \frac{1}{\rho} + j\omega \varepsilon_{r;h}\varepsilon_0 \ , \qquad (4)\\ \eta_v = \frac{1}{\rho \lambda^2} + j\omega\varepsilon_{r;v}\varepsilon_0 \ . \qquad (5)\end{split}\]

With this function we recompute it. We replace the real part, the resistivity \(\rho\), in equations (4) and (5) by the complex, frequency-dependent Cole-Cole resistivity [\(\rho(\omega)\)], as given, for instance, in equations (1)-(3). Then we add back the imaginary part coming from thet dielectric permittivity (basically zero for low frequencies).

Note that in this notebook we use this hook to model relaxation in the low frequency spectrum for IP measurements, replacing \(\rho\) by a frequency-dependent model \(\rho(\omega)\). However, this could also be used to model dielectric phenomena in the high frequency spectrum, or for IP measurements in very resisitive ground where the permittivity may be included. Therefore, we also provide a Cole-Cole function for permittivity, which treats the conductivity as constant with frequency, and adds the frequency-dependent complex permittivity, i.e., \(\varepsilon_r\) is replaced by a frequency-dependent formula \(\varepsilon_r(\omega)\).

def cole_cole(inp, p_dict):
    """Cole and Cole (1941)."""

    # Compute complex conductivity from Cole-Cole
    iotc = np.outer(2j*np.pi*p_dict['freq'], inp['tau'])**inp['c']
    condH = inp['cond_8'] + (inp['cond_0']-inp['cond_8'])/(1+iotc)
    condV = condH/p_dict['aniso']**2

    # Add electric permittivity contribution
    etaH = condH + 1j*p_dict['etaH'].imag
    etaV = condV + 1j*p_dict['etaV'].imag

    return etaH, etaV


def pelton_et_al(inp, p_dict):
    """ Pelton et al. (1978)."""

    # Compute complex resistivity from Pelton et al.
    iotc = np.outer(2j*np.pi*p_dict['freq'], inp['tau'])**inp['c']
    rhoH = inp['rho_0']*(1 - inp['m']*(1 - 1/(1 + iotc)))
    rhoV = rhoH*p_dict['aniso']**2

    # Add electric permittivity contribution
    etaH = 1/rhoH + 1j*p_dict['etaH'].imag
    etaV = 1/rhoV + 1j*p_dict['etaV'].imag

    return etaH, etaV


def cole_perm(inp, p_dict):
    """ Cole and Cole (1941)."""

    iotc = np.outer(2j*np.pi*p_dict['freq'], inp['tau'])**inp['c']

    jw = np.outer(2j*np.pi*p_dict['freq'], np.ones(2))

    # Compute the complex admittivity described by a
    # constant (DC) conductivity and the Cole-Cole permittivity

    epsilonH = inp['eperm_8'] + (inp['eperm_0']-inp['eperm_8'])/(1 + iotc)
    epsilonV = epsilonH/p_dict['aniso']**2

    etaH = 1/inp['rho_0'] + jw*epsilonH
    etaV = 1/inp['rho_0'] + jw*epsilonV

    return etaH, etaV

Example#

Two half-space model, air above earth:

x-directed sourcer at the surface
x-directed receiver, also at the surface, inline at an offset of 500 m.
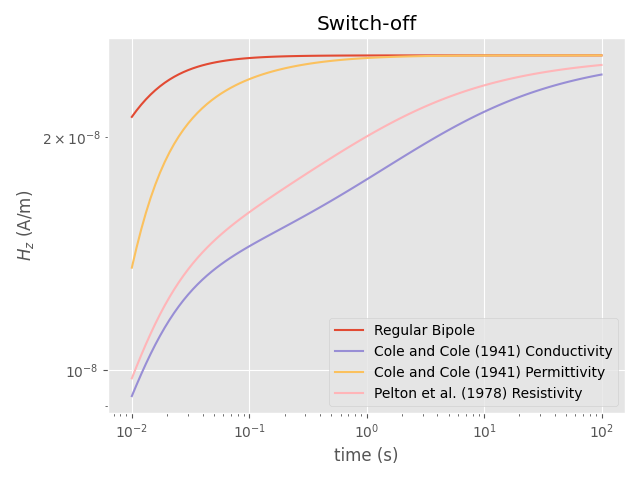
Switch-on time-domain response
Isotropic
Model [air, subsurface]
- \(\rho_\infty = 1/\sigma_\infty =\) [2e14, 10]
- \(\rho_0 = 1/\sigma_0 =\) [2e14, 5]
- \(\tau =\) [0, 1]
- \(c =\) [0, 0.5]

# Times
times = np.logspace(-2, 2, 101)

# Model parameter which apply for all
model = {
    'src': [0, 0, 1e-5, 0, 0],
    'rec': [500, 0, 1e-5, 0, 0],
    'depth': 0,
    'freqtime': times,
    'signal': 1,
    'verb': 1
}

# Collect Cole-Cole models
res_0 = np.array([2e14, 10])
res_8 = np.array([2e14, 5])
tau = [0, 1]
c = [0, 0.5]
m = (res_0-res_8)/res_0

e0 = 8.85e-12  # Vacuum permittivity
eperm_0 = e0*np.array([1, 6e08])
eperm_8 = e0*np.array([1, 3])


m = (res_0-res_8)/res_0

cole_model = {'res': res_0, 'cond_0': 1/res_0, 'cond_8': 1/res_8,
              'tau': tau, 'c': c, 'func_eta': cole_cole}

cole_perm_model = {'res': res_0, 'rho_0': res_0, 'eperm_0': eperm_0,
                   'eperm_8': eperm_8,
                   'tau': tau, 'c': c, 'func_eta': cole_perm}

pelton_model = {'res': res_0, 'rho_0': res_0, 'm': m,
                'tau': tau, 'c': c, 'func_eta': pelton_et_al}

# Compute
out_bipole = empymod.bipole(res=res_0, **model)
out_cole = empymod.bipole(res=cole_model, **model)
out_cole_perm = empymod.bipole(res=cole_perm_model, **model)
out_pelton = empymod.bipole(res=pelton_model, **model)


# Plot


def pos(data):
    """Return positive data; set negative data to NaN."""
    return np.where(data > 0, data, np.nan)


plt.figure(constrained_layout=True)
plt.title('Switch-off')
plt.plot(times, pos(out_bipole), '-', label='Regular Bipole')
plt.plot(times, pos(-out_bipole), '--', label='')

plt.plot(times, pos(out_cole), '-', label='Cole and Cole (1941) Conductivity')
plt.plot(times, pos(-out_cole), '--', label='')

plt.plot(times, pos(out_cole_perm), '-',
         label='Cole and Cole (1941) Permittivity')
plt.plot(times, pos(-out_cole_perm), '--', label='')

plt.plot(times, pos(out_pelton), '-', label='Pelton et al. (1978) Resistivity')
plt.plot(times, pos(-out_pelton), '--', label='')

plt.legend()
plt.yscale('log')
plt.xscale('log')
plt.ylabel('$H_z$ (A/m)')
plt.xlabel('time (s)')

empymod.Report()

Wed Mar 12 21:10:32 2025 UTC
OS	Linux (Ubuntu 22.04)	CPU(s)	2	Machine	x86_64
Architecture	64bit	RAM	7.6 GiB	Environment	Python
File system	ext4
Python 3.11.10 (main, Nov 5 2024, 16:13:19) [GCC 11.4.0]
numpy	2.1.3	scipy	1.15.2	numba	0.61.0
empymod	2.5.1	libdlf	0.3.0	IPython	9.0.2
matplotlib	3.10.1